Paul Marmet
This paper shows that the phenomena usually attributed to relativity are a simple consequence of mass-energy conservation. When atoms are accelerated, the increase of kinetic energy increases the electron mass, which makes the Bohr radius larger. This increase of radius produces a shift in the atomic energy levels and also an increase of the physical size of matter. Consequently, a moving atomic clock now runs at a different rate. Quite naturally and without Einstein's relativity, we see how the increase of size of the Bohr radius and of macroscopic matter, are exactly equal to Einstein's prediction. Einstein's theory of relativity predicts length contraction, but does not explain how matter can be physically contracted or why this phenomenon is not reversible when the mass in the moving frame is accelerated back to the original frame. Einstein's length contraction implies that the Bohr atom gets smaller. However, quantum mechanics shows that such a contraction of the Bohr radius should increase the atomic energy levels. This consequence of Einstein's predictions is contrary to observational facts, which show that, at high velocity, the atomic energy levels become smaller and the atomic clocks get slower. The mechanism of dilation and contraction of matter is logically explained here, using Newton physics and the fundamental principles of quantum mechanics. Using the de Broglie equation, we calculate the relationship between the Bohr radii in different frames, which is responsible for the physical change of length of matter, in agreement with all observational data. Furthermore, just as for mass and energy units, we show that the physical size of the Planck unit, needs to increase g times with velocity. Observations previously attributed to relativity can now be explained logically. These results are also compatible with a rational explanation of the advance of the perihelion of Mercury around the Sun. We must conclude that there exists no space-time distortion and the Einstein's relativity principle cannot be valid. Everything is naturally explained as a change of size of matter and a change of clock rate. A corresponding solution also exists in the case of gravitational energy as will be demonstrated in a future paper. These phenomena, taking place in atoms are also predictable in the nucleus of matter. For the same reason, the lifetimes of radioactive nuclear states also changes naturally with velocity and potential energy.
1- Introduction.
The
problem of dilation and contraction of matter in relativity could never be
explained logically. Einstein's relativity presents no physical
rationalization explaining why and how matter can dilate or
contract. That field of physics is impenetrable, because it is not
compatible with the existence of a physical reality, independent of the
observer's existence. Einstein's theory has never been expressed
unequivocally and the more recent theoretical developments collapse into a
deeper mystery. Unfortunately, just as during the Middle Ages, most
scientists accept the idea that nature is not compatible with conventional
logic. Nowadays, most scientists ignore or refuse to read papers
implying an existence of matter independent of the
observer.
In this
paper, the phenomenon of length contraction or dilation is explained
logically without any of Einstein's relativity hypotheses
(1). Everything is explained as a
function of the physics of Newton, Coulomb and de Broglie. Due to
the increase of kinetic energy and the application of the principle of
mass-energy conservation, we see that the Bohr radius increases, so that
the physical size of matter increases. This dilation of matter is
not a simple mathematical transformation visible by only one observer in a
specific frame, it is a physical reality. Also, matter shrinks back
to its original length when the velocity is reduced. The fundamental
principles related to this natural phenomenon have been explained
previously (2).
The
fundamental reason for which the Bohr radius increases when kinetic energy
is given to the atom is mechanical. In a few words, atoms in space
are like gyroscopes moving freely in space. The orbiting electron
around the nucleus represents the spinning wheel. When the mass of
the spinning wheel (here the orbiting electron inside an atom) increases,
the velocity of rotation decreases, due to momentum conservation.
Therefore in the Bohr atom, when the electron mass increases, the electron
velocity decreases. Using Coulomb forces, it is well known that the
radius of the electron orbit is larger when the electron velocity becomes
slower. Consequently, the Bohr radius becomes larger when the atom
is moving faster. The change of Bohr radius is the fundamental cause
of dilation of matter when atoms acquire kinetic energy. This
mechanism is calculated in detail in this paper.
In
agreement with observations, we show also that, even if in fact the
physical size of the atom is increasing, the quantum structure of the
moving atom is changing in such a way that these changes of mass and
length remain generally undetectable to the moving observer. The
esoteric Einstein's hypothesis of space-time distortion is unacceptable,
because it is not compatible with a physical reality independent of the
observer. Contrary to most papers in modern physics, we always refer
here to a realistic physical model. We question the physical
interpretation of equations. There must be no mathematical model in
physics, without being logically supported by a physical model. One
of the most important errors in Einstein's relativity is that, the
inevitable change of sizes of some moving reference units (i.e. the Planck
constant) are disregarded.
We
show here that all phenomena previously attributed to Einstein's
relativity are in fact, the simple consequence of application of the
principle of mass-energy conservation in atoms and molecules. There
is no time dilation or space contraction. There is only a change of
clock rate and a change of length of matter due to the change of Bohr
radius.
2 -Fundamental
Mechanisms Inside Atoms.
The complex
internal structure of atoms and molecules is nothing but the sum of a few
simple fundamental relationships. The best way to verify the
compatibility between all these fundamental relationships and experimental
data is with simple atoms, in which each individual phenomenon is
recognizable independently. For example, it is well known that all
the deepest fundamental physics phenomena involved in the structure of
complex matter, appear under their simplest fundamental form in atomic
hydrogen. Inside the hydrogen atom, we know that the Coulomb
attracting force between the two charged particles (electron and the
proton) is equal to the Newton centrifugal force of the orbiting
electron. This was recognized by Bohr. We have:
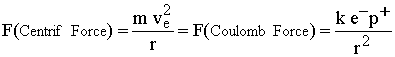 1
1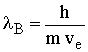 and
and Equations 1 and 2 are in a perfect agreement with experiments when the atom is stationary. It is also an experimental fact that when an atom is in motion, the same relationships are compatible within the moving atom, if we use the relevant moving reference units [v]. However, we have seen previously (2) that in fact, the moving atoms are unquestionably different, due to the absorbed kinetic energy, which gives an extra mass to the electron and to the nucleus. The resulting change of size of the reference units is due to the increase of electron mass. These previously ignored absolute physical modifications between frames are the origin of the non-realistic relativity principle hypothesized by Einstein. In order to take into account that both matter and the size of the reference units are changing simultaneously with velocity, we must note that a physical quantity cannot be defined as a simple "number of reference units" as generally used in papers. In contrast with a mathematical quantity, we must define a physical quantity. A physical quantity is an absolute quantity, defined as the product of the number of units, multiplied by the size of the corresponding reference unit.
Due to the increase of mass with velocity, the size of the reference unit is changing in different frames. This variation of size of reference units must be taken into account. We have seen previously (2), that we need a double index to get the relevant information on the physical quantity being measured. For example, we see that the number representing a mass m, can have four different values, depending on the frame where it is located and the reference unit used to measure it. We can have ms[s], ms[v], mv[s] and mv[v]. The subscript after the physical quantity refers to the frame where the particle is located. The subscript s means that the particle is located in the stationary frame, and the subscript v means that the particle is located in the moving frame. Furthermore, the physical quantity is also followed by a square parenthesis, which indicates the size of the fundamental reference unit used to express that physical quantity. The index [s] means that the corresponding reference unit used is in the stationary frame. The index [v] means that the reference unit used for that measurement is in the moving frame.
We will see that there exist naturally three different situations when matter moves to a moving frame. In most cases, an absolute physical quantity like a mass m, is the product of the number of units (ms or mv) times the size of the unit used to measure it, which is [s] or [v]. For example, an absolute physical length like rs[v] is the product of the number of units rs, times the size of the unit [v]. In the second situation, the absolute size of the Coulomb and the Planck constants must be considered when switching frames. In the Coulomb case, nothing changes neither physically nor mathematically. This is the case for the electric charges e- and protons p+. In that case, indexes are irrelevant here, since the number of units and the size of units are identical in all frames at any velocity. It is well known that the absolute electric charge of electrons and protons is constant when the particle is accelerated to high velocity. This is an experimental fact, since observational data have shown that, when an electron is accelerated to a high velocity and then deflected in a magnetic field, the electron "charge to mass ratio" (e/m) is changing in a way, which is exactly compatible with the expected increase of mass, assuming a constant electric charge and mass-energy conservation. Consequently, we have:
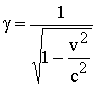 6
6In physics, the parameters in equations generally represent the number of standard units, (independently of the size of the unit). It is arbitrarily assumed that the size of the reference unit is constant in different frames. However, it is not so when a moving observer is moving with the mass, because the reference units in the moving frame are different, due to their kinetic energy. Then, the number (alone) of units, to measure masses, lengths and clock rates is insufficient to represent a physical quantity.
An example would be useful. Let us consider a rod having a length of 2.4 meters when measured in a stationary frame with respect to a reference meter also in the same frame. This length is written 2.4 ms[s]. If furthermore, that rod is carried to a frame moving at velocity v and is measured with respect to the reference meter also in the local frame (the moving frame), the length of the same rod will be given as 2.4 mv[v]. We see that, in both cases, the length of the rod is mathematically the same (i.e. 2.4 local meters). However, the physical length of the rod is certainly different in the moving frame. Also, the physical length given by g times 2.4 ms[s] is equal to 2.4 mv[v]. Furthermore, the physical length 2.4 mv[s] equals 2.4 mv[v]. The reader must cautiously perceive the difference between the mathematical equality and the physical equality. Realistically, numbers are the only things mathematical equations are calculating.
The usual equations in physics completely rely on an assumption of a definition of a reference unit, which is assumed to be constant in any frame. This hypothesis is erroneous. That hypothesis is not compatible with the principle of mass-energy conservation (2).
The parameters in a normal mathematical equation give nothing but the number of units rather than the size of the physical quantity. In previous papers (2, 4-7), the same number of units was instead represented by the notation N-r, N-m and N-E.
3 - The Coulomb Energy
Curve
Atom at Rest. - The equilibrium between the centrifugal force and the electric
force between the electron and the nucleus is described in the Bohr
model. This is somewhat similar to the attracting gravitational
force between the orbiting planets around the Sun as presented by Gerhard
Herzberg (3) and others. When the
atom is stationary, equation 1 gives the relationship between the radius r
of the orbiting electron as a function of the orbiting velocity
ve. From equation 1 we
get:
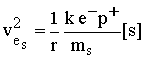 7
7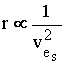 8
8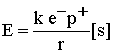 9
9Atom in Motion. - When an atom is in motion, due to the kinetic energy transferred from the external frame, (which is added to the particle), the principle of mass-energy conservation requires that the mass of all particles increases. Therefore, as given by equation 5, the electron mass increases inside the atom, due to the higher velocity of the atom, just as the proton mass. Let us calculate the change of the electron orbital velocity inside the atom, and around the nucleus, due to the increase of electron mass (from ms[s] to gms[s]). Substituting gms[s] in equation 7 gives:
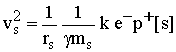 10
10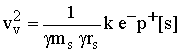 12
12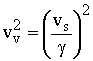 13
13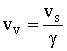 14
14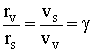 15
15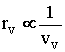 16
16
Figure 1
Index
|||||
CD-ROM
![]()
|||||
FAQ
|||||
Photographs
Meeting
Italy,
|||||
Photographs
Meeting
London
|||||
1A-
Einstein's
Theory
of
Relativity
versus
Classical
Mechanics
Preface
Contents
Chap#1
Chap#2
Chap#3
Chap#4
Chap$5
Chap#6
Chap#7
Chap#8
Chap#9
Chap#10
Chap#11
Chap#12
Appendix1
Appendix2
|||||
1-A-X
Fundamental
Nature of
Relativistic
Mass
and
Magnetic
Fields.
|||||
1B-
The
GPS
and
the
Constant
Velocity
of
Light.
|||||
1C-
A
Detailed
Classical
Description
of
the
Advance
of
the
Perihelion
of
Mercury
|||||
1D-
Relativistic
Deflection
of
Light
Near
the
Sun
Using
Radio
Signals
and
Visible
Light.
|||||
|||||
1F
Natural
Physical
Length
Contraction
Due
to
Gravity
|||||
1G
Anomalous
Acceleration
of
Pioneer
10
and
11
|||||
2-
in
Modern
Physics:
A
Solution.
Preface
Contents
Index
Chap#1
Chap#2
Chap#3
Chap#4
Chap#5
Chap#6
Chap#7
Chap#8
Appendix
|||||
3-
A
New
Non-
Doppler
Redshift
|||||
4A-
Big
Bang
Cosmology
Meets
an
Astro-
nomical
Death.
|||||
4B-
Discovery
of H2
in
Space
Explains
Dark
Matter
and
Redshift.
|||||
5-
The
Origin
of
the
3
K
Radiation.
|||||
6-
Quantum
Mechanics
and
its
Paradox:
A
Realistic
Solution
to
Mermin's
EPR
Apparatus.
|||||
7-
Enlarge-
ment
of
the
Earth's
Shadow
on
the
Moon:
An
Optical
Illusion.
|||||
8-
Redshift
of
Spectral
lines
in the
Sun's
Chromos-
phere.
|||||
9-
Non-
Doppler
Redshift
of
Some
Galactic
Objects.
|||||
10-
Stellar
Aberration
and
Einstein's
Relativity.
|||||
11-
Incompati-
bility
between
Einstein's
General
Relativity
and
the
Principle
of
Equi-
valence
|||||
12-
Cosmic
Matter and
the
Non-
expanding
Universe.
|||||
13 -
The 3
K
Microwave
Background and
Olbers'
Paradox.
|||||
14 -
The
Cosmolo-
gical
Constant
and
the
Redshift
of
Quasars.
|||||
Return
to:
Top this
Page
|||||
About
the
author:
Paul
Marmet |||||
Canadian
Who's
Who
Ed.
2001
|||||
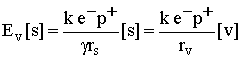 17
17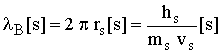 19
19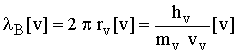 20
20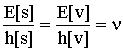 24
24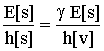 26
26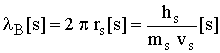 28
28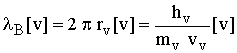 29
29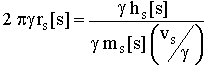 34
34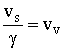 37
37